Understanding the Fundamental Mechanism of Intelligence
Neurithmic Systems's goal is to understand the mechanism of intelligence. Since the brain is the only known thing that possesses true intelligence and since the brain's cortex is the locus of memory, reasoning, etc., our goal reduces to discovering the fundamental nature of cortical computation. Perhaps the most salient property of the ~2mm thick sheet of neurons/neuropil that comprises the cortex is its extremely regular structure over most of its extent, i.e., 6-layer isocortex (but even the older non-isocortex areas, e.g. paleo/archi-cortex has very regular structure that is phylogenetically and systematically related to isocortex). The gross anatomical/circuit motif repeats on the minicolumnar (~20-30 um) scale throughout isocortex. And there is appreciable evidence for functional / structural repetition at the macrocolumnar ("mac") scale (~300-500 um) as well, e.g., hypercolumns of V1, barrel-related columns of rodent S1 (e.g., Figure 1).
We believe that the mac is the fundamental computational module of cortex and Neurithmic's Sparsey® model is proposed to capture the essential computational nature of the cortical mac (see model overview).
Why is there not yet more evidence for mac-scale functional modules throughout all of cortex?
We argue that the most essential property of neural, more specifically cortical, computation is that it uses sparse distributed representations (SDR), a.k.a., sparse distributed codes (SDC). The reason is that SDR admits an algorithm, Sparsey's Code Selection Algorithm (CSA), possessing the following powerful and unique properties:
- "Fixed" time complexity storage and best-match retrieval: We define this as: The number of steps needed to both store a new item into and retrieve the best-matching item from a database (in Sparsey, a mac) remains constant as the number of items in the database grows, up to a maximum, N, which depends on the size (dominated by the number of weights, W) of the model.
- Fixed time complexity belief update: the likelihood distribution over all hypotheses stored in a database (mac) is updated in fixed time, in fact, in the same time that it takes to find the single best-matching item. This operation is called belief update in the Bayesian Net literature.
Several points are immediately in order:
- The above statements apply for both spatial and spatiotemporal patterns, i.e., multivariate sequences. From its inception, Sparsey was developed, first and foremost, to process spatiotemporal patterns.
- The above statements do not mean the CSA has constant ["O(1)"] time complexity for these operations, wherein the number of steps needed remains constant as the number of stored items grows without bound. In fact, no algorithm attains this "Holy Grail" capability. In particular, Hashing has O(1) time complexity storage and exact-match retrieval, but not O(1) best-match retrieval. And tree-based methods at best have logarithmic time complexity for both storage and best-match retrieval.
- Though weaker than constant time complexity, fixed time complexity storage, best-match retrieval, and belief update may have great utility and scalability if it can be demonstrated that N grows sufficiently rapidly in W. Furthermore, if SDR-based modules such as described here (each one of which performs these operations in fixed time) are arranged into large many-leveled hierarchies (a tiny example of such is shown in Figure 2; and see sketch of mapping of Sparsey to cortex), then:
- The ultimate assessment of how information storage capacity of the whole model scales with overall model size, will depend on numerous parameters both of individual macs and of the inter-mac connectivities / communications. In particular, in an overall hierarchical context in which compositionality is appropriately exploited, the amount of information that any individual mac at any given level must be able to store (or in other words, the size of the basis it needs to hold), may be relatively small, e.g., up to say several hundreds of stored codes (each one representing a basis vector).
- Yet, the model as a whole retains its fixed time complexity because a whole-model storage, retrieval, or belief update operation involves a single iteration over the fixed total number, M, of macs, each of which has fixed time complexity, and multiplication by a constant, M, does not change an algorithm's time complexity.
- Here is a more detailed explanation of how hierarchy may effectively confer true O(1) time complexity learning and best-match retrieval, for sequences, throughout long lifetimes operating in natural worlds (i.e., worlds with natural, i.e., 1/f, statistics).
- No other computational method has been shown to have fixed-time storage and best-match retrieval, nor fixed time belief update. In particular, despite their impressive successes, it has not been shown for any Deep Learning (DL) model. Direct comparison of learning time complexity between a model like Sparsey, which does single-trial, on-line learning and most other machine learning (ML) models is difficult. This is because most other ML models, including DL and SVM models, are designed to learn class boundaries but generally not to permanently store retrievable traces of the individual items stored. In other words, historically, most ML (and pattern recognition) models have sought to explain only semantic memory, i.e., knowledge of class/similarity structure of the input space, but not also episodic memory, which is detailed memory of the specific items experienced. Nevertheless, it is widely acknowledged that DL training times can be very long and that DL's tractability depends on massive machine parallelism (e.g., GPU computing) and the availability of massive amounts of training data. We believe this may in fact belie the fundamentally
- Non-biological nature of ConvNets and
- Potential limitations of Deep Learning
and related models. As any computer scientist knows, as you scale to progressively larger problem instances, the lowest complexity algorithm (especially time complexity, given the rapidly descreasing cost of storage) eventually beats all others. Given the growing awareness of the need to mine truly massive amounts of data in order to get the best answers, e.g., for financial/economic prediction, or for searching biological sequence domains, etc., a model with "fixed" time complexity storage and best-match retrieval for sequential data, such as Sparsey, holds great promise.
- To our knowledge, no existing DL model, RBM-based or ConvNet-based, uses SDR. It is therefore unsurpising that no DL model (nor any other ML model) has been shown to have fixed time complexity storage, best-match retrieval, and belief update. Note: the sparse coding concept (cf. Olshausen & Field) is widely used throughout ML, and specifically neuromorphic, modeling, but:
Sparse Coding ≠ Sparse Disributed Representations!
- Very few ML models, even specifically neuromorphic models, including the DL models, explicitly enforce mesoscale, e.g., macrocolumn-scale, structure or function (See discussion here).
- The constant, N, in the definition of fixed time compexity, is not a hard limit on the number of items that can be stored per se, but rather a value above which the quality/correctness of retrievals will fall below some statistically ensured criterion.
- Sparsey's best-match (closest-match, nearest-neighbor) retrieval capability results from the fact that the CSA implements a similarity-preserving mapping of inputs to codes. Thus, a mac automatically learns/embeds a (generally spatiotemporal) similarity metric from the set of inputs it experiences. Neither the intrinsic dimensionality of the eventually-learned metric nor the maximum order of the statistics learnable are fixed. Arbitrarily nonlinear category boundaries can be learned via a supervised protocol operating between/amongst multiple macs.
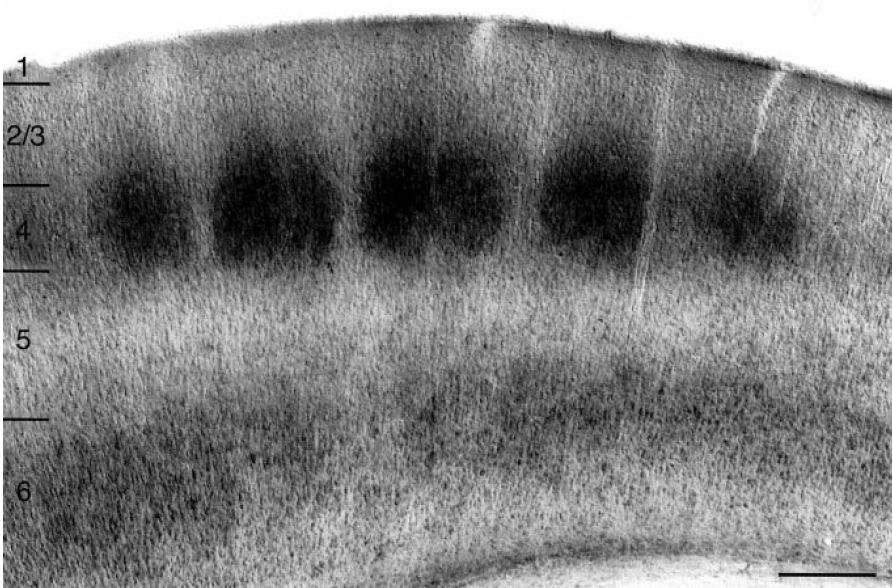
Figure 1: From Lubke et al 2000. Cytochrome Oxidase staining of Rat S1 ("barrel cortex"), shows macrocolumn-scale functional/structural organization. Scale bar: 500um.
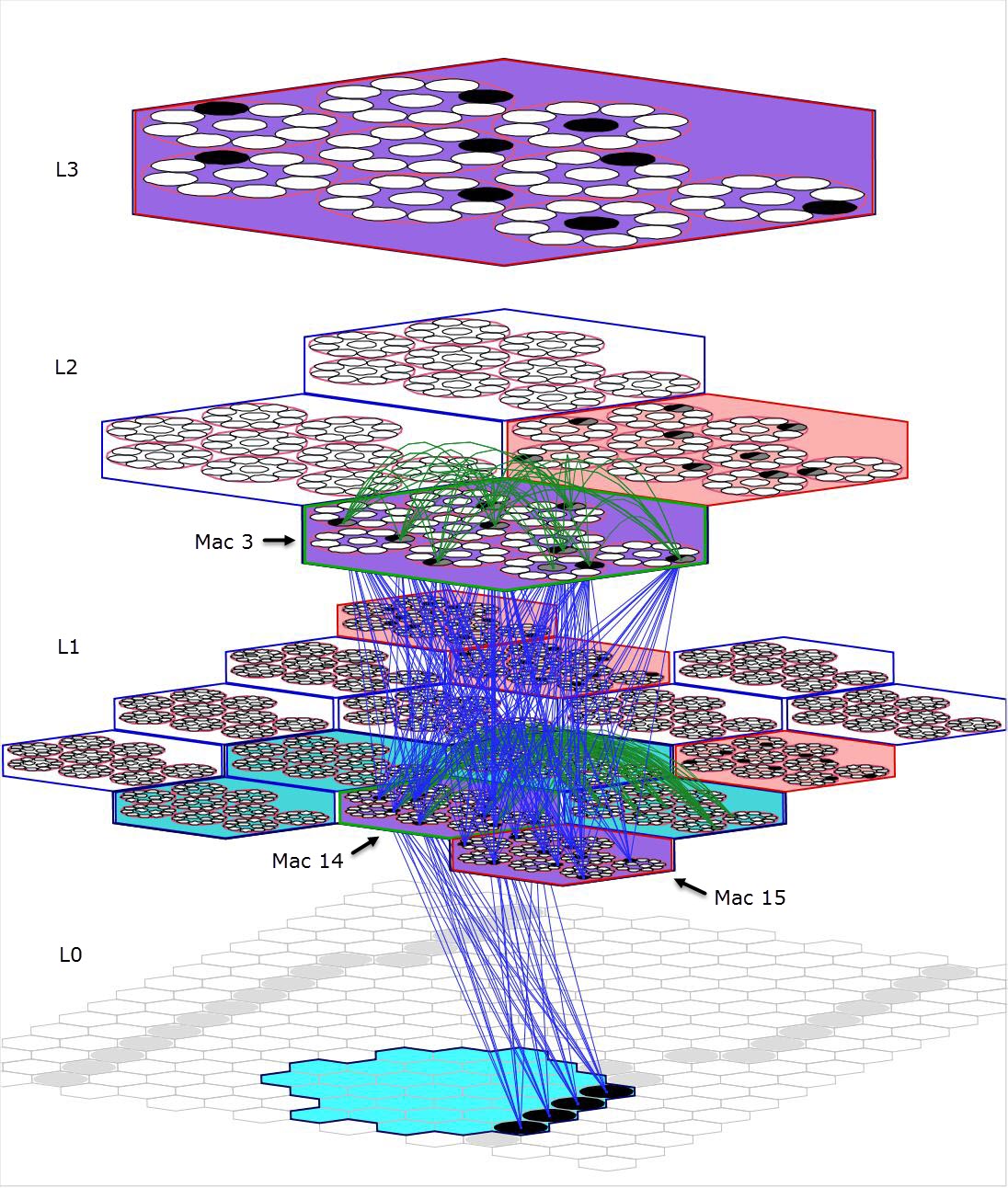
Figure 2: A tiny instance of a Sparsey® network with a 16x16 pixel input level (L0) and three internal levels with a total of 21 macs. The cyan patch at L0 is the RF of L1 mac 14. That mac is active because an appropriate number of pixels in its RF are active (black). L2 mac 3 is active because an appropriate number (two, L1 macs 14 and 15) of the six L1 macs comprising its immediate RF (cyan and purple) are active, and similarly for the L3 mac. Representative samples of the U-wts leading to L1 mac 14 and L2 mac 3 are shown, as well as some horizontal (H) wts. Top-down (D) wts are not shown here. We discuss parameters and features of many other figures like this throughout these pages.
Figure 3: Mac RFs can in general overlap. The three frames do not show successive processing moments in the model, but rather emphasize the RFs of three different macs active on the same time step to show how their RFs, in particular, their bottom-up RFs (URFs), overlap. (The animation runs smoothly in Chrome/IE, but seems to to jump a bit in Firefox. Try usng pause control and clicking slider to dwell on the different URFs.) Note in particular, that although L1 macs 14 and 15 have quite different URFs, they are activated by almost the same pixels in this instance. For mac 14, the input could be described as a "vertical edge at the right edge of the URF", whereas for mac 15, it would be described as a "vertical edge in the center of the URF". It's essentially the same feature, but encoded redundantly in macs 14 and 15: of course, the SDR codes assigned in each mac are disjoint and not intrinsically related. Both of these L1 codes are associated with a single code stored in L2 mac 3. The redundancy here underlies a meta-level of overcompleteness. The third frame shows the L1 and L2 URFs for L2 mac 1. There's lots more to say on the topic of overlapping RFs.
