Storage Capacity of a whole Hierarchy of Macrocolumns

This page has my general argument that for naturalistic input domains, a hierarchy of macrocolumns could operate indefinitely storing all novel, important inputs, without ever reaching capacity, and operating with O(1) time complexity for both learning and best-match retrieval.

My prior work has demonstrated that Sparsey’s core algorithm (for learning and inference) runs in fixed time, i.e., the number of operations needed either to store a new item or retrieve the best-matching item remains fixed as the number of stored items increases. A Sparsey mac (SDR coding field) is an associative memory in which items (memory traces) are stored in superposition. Thus, as the number of items stored grows, interference (crosstalk) will increase, reducing the average retrieval accuracy over the set of stored items. We define a mac's storage capacity to be the number of items that can be safely stored, i.e., stored so that average retrieval accuracy over all stored items exceeds a defined threshold, e.g., 97%. Figure 1 (from 1996 Thesis) shows that a mac's storage capacity scales linearly in the weights (it also scales super-linearly in the units) (see here for more detail).

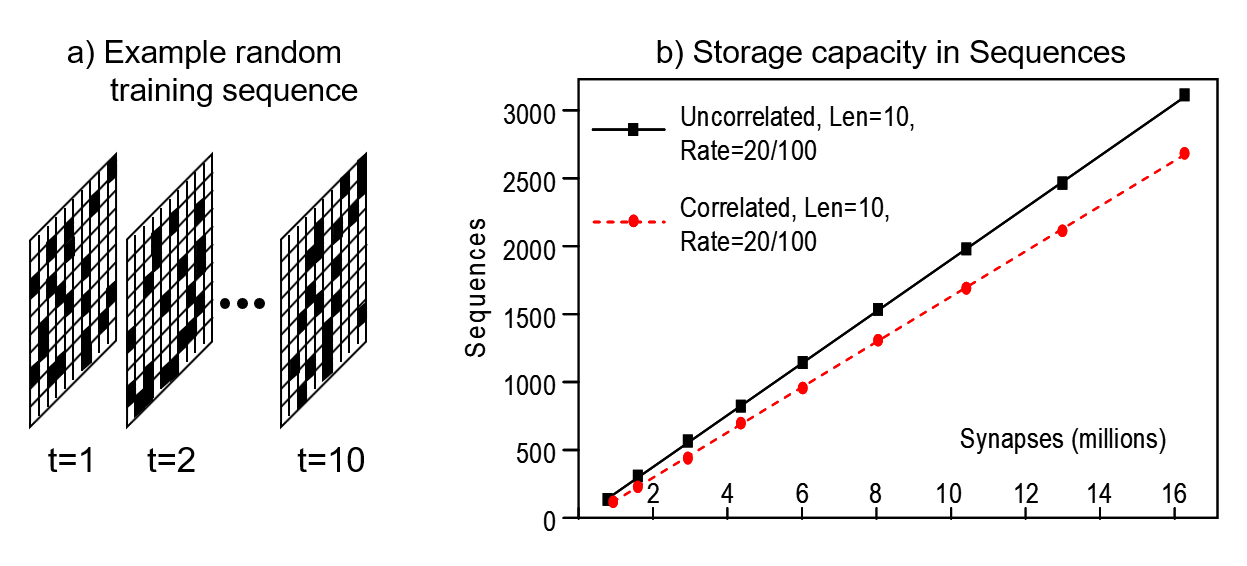
Figure 1: Sparsey storage capacity results for synthetic random sequences. (a) Example random sequence. 20 out of 100 pixels randomly chosen on each of 10 frames. (b) Capacity grows linearly in the weights. "Correlated" refers to the "complex sequence" case, i.e., where we predefine an alphabet (lexicon) of frames (in these experiments, lexicon size was 100), and then sequences are created by drawing 10 frames randomly with replacement from lexicon.

The inverse of a linear relation is also linear. Thus the the graph in Figure 1 also says that the number of weights needed to safely store N items grows linearly [O(N)] in the number of items (sequences), N. And, since the number of steps needed to store or best-match retrieve an item is dominated by a single iteration over the weights to the mac (i.e., each cell must sum its inputs), an individual mac has O(N) time complexity for both storage (learning) and best-match retrieval. However, we emphasize that for any fixed-size mac (fixed number of afferent weights), the number of steps needed to perform either operation (thus, the response time) remains constant as the number of stored items grows. While tree-based methods and locality-sensitive hashing (LSH) have better time complexity, O(logN), the number of steps needed grows as the number of items stored grows.

Thus, if we could be sure that a Sparsey mac will never be required to store more items than its capacity over its entire lifetime, then that mac would effectively possess constant, i.e., [O(1)], time complexity for both operations. As Figure 1 shows, the storage capacity of a single mac does scale well, and so a fixed, finite capacity, could be acceptable for certain limited applications. But it does not suffice for a fully autonomous AGI (artificial general intelligence) system operating indefinitely in the wild. No algorithm has been shown to possess true O(1) time complexity for both storage and best-match retrieval: it's unlikely one exists. However, we can achieve something quite close. Specifically, if an overall AGI system is a hierarchy of macs, then principles can be leveraged (described below) whereby the expected time for the system as a whole to reach its storage capacity increases exponentially in system size, where the size measure reflects number of total number of weights and the number of levels. Such a relationship, i.e., exponential growth of operational lifetime in system size (physical resources), while retaining fixed response time for learning and best-match retrieval, makes scaling to arbitrarily large data/problem size practical.

Specifically, our constructive argument involves a hierarchy of macs operating in a naturalistic domain, i.e., a domain whose objects/events have a recursive, part-whole, compositional (hierarchical) structure (which generates 1/f statistics), in which:

1. no individual mac ever exceeds its capacity (thus there is no catastrophic forgetting),
2. the rate at which macs approach capacity, i.e., the rate of occurrence of inputs that are sufficiently novel to require being stored decreases exponentially with level; and
3. processing (learning/retrieving) an input entails a single iteration over all the macs, i.e., a single bottom-up, level-by-level processing pass over all the macs.

We refer to such a system as effectively possessing O(1) time complexity storage and best-match retrieval. Point 3 is needed because if the run time of each mac is fixed, then the sum of the run times of all macs is also fixed. Indeed, Sparsey's algorithm satisfies Point 3. Furthermore, in practice, as can be seen in many of this website's animations, only a small fraction of the macs activate, and thus contribute to run time, on each time step. [Furthermore, it is not necessary that a processing pass be limited to only a single iteration over all macs (though that is the case for the current version of Sparsey): any fixed number of iterations over the macs implies that the total processing time is fixed.]

With regard to Point 1, there are two scenarios by which a mac can avoid exceeding capacity over the lifetime of the overall model. Either: A) we can "freeze" the mac when it reaches capacity, preventing any further codes from being stored in it; or B) it can happen that due to the combined effects of i) the strong structural constraints of natural domains, and ii) the further constraining effects of filtering through lower levels, the set of novel inputs arriving at a higher-level mac over a long lifetime is smaller than the mac's fixed capacity. Broadly, scenario A dominates in the lower level macs and scenario B dominates at the higher levels. Part of the reason scenario B dominates in higher level macs is the freezing that occurs in lower level macs.

First we consider the lower level macs. For concreteness, let's consider the first internal level (L1) of macs, e.g., V1. An L1 mac has a small receptive field (RF), i.e., a small aperture onto the visual field.  Sparsey assumes the input level (L0) is an array of binary pixels. Thus, an L1 mac's RF might be a 8x8-pixel patch of the input level. Furthermore, we assume input video frames are preprocessed by being edge-filtered, binarized, and skeletonized (all extremely cheap, local operations).  For naturalistic video and such a small aperture, this generally yields frames containing one/few edge segments, often with quite low curvature. Figure 2a shows examples of such inputs. Figure 2b shows examples of inputs that would be extremely unlikely to occur given the operation of this preprocessing on a domain with naturalistic statistics.

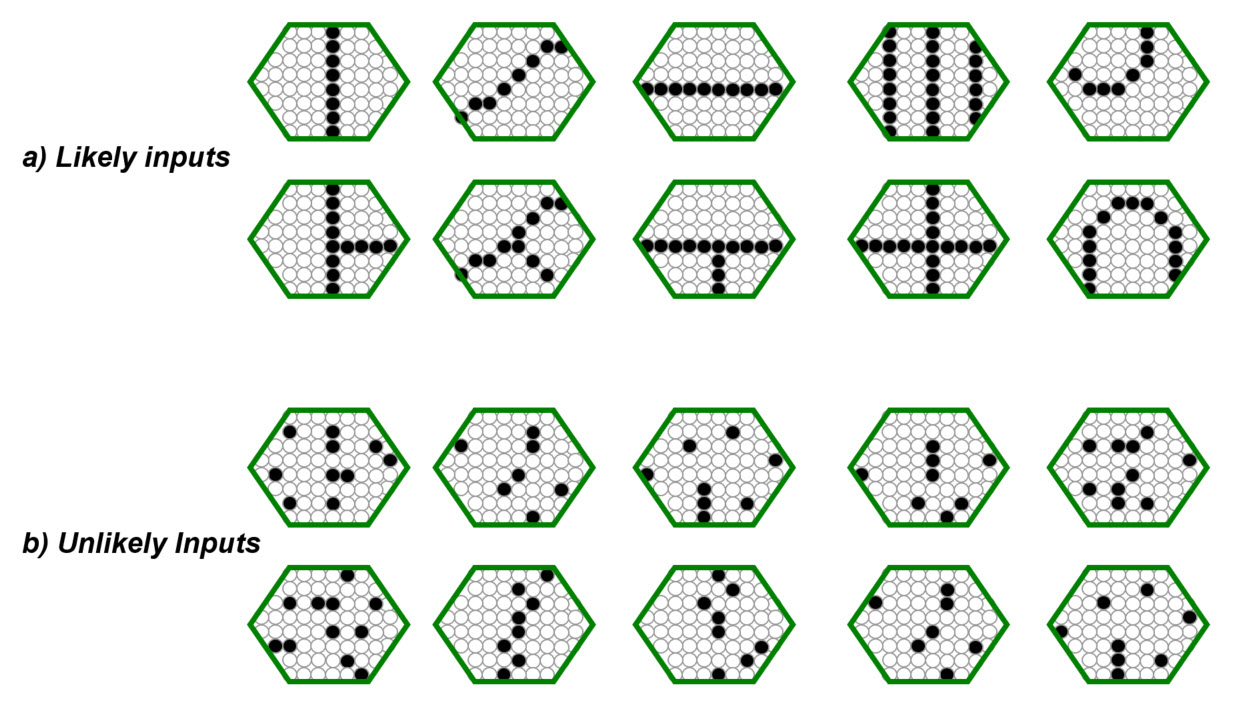
Figure 2: Possible input patterns (features), assuming the described preprocessing, for a hexagonal RF of about 70 pixels. (a) Features likely to occur. (b) Features not likely to occur.

In addition, Sparsey implements the policy that a mac only activates if the number of active units in its RF is within a small range. Consider a smaller hexagonal RF with 37 pixels (approx. 6x6) and suppose the range is [9,10], i.e., an SDR is only activated in the mac if 9 or 10 pixels are active in its RF.  In that case, there are C(37,9) + C(37,10) = ~473 million possible input patterns for which the mac will become active. However, given the preprocessing, only a small fraction of those, perhaps in the tens or hundreds of thousands, are likely to ever occur.  Figure 3 shows some examples of patterns that might occur.

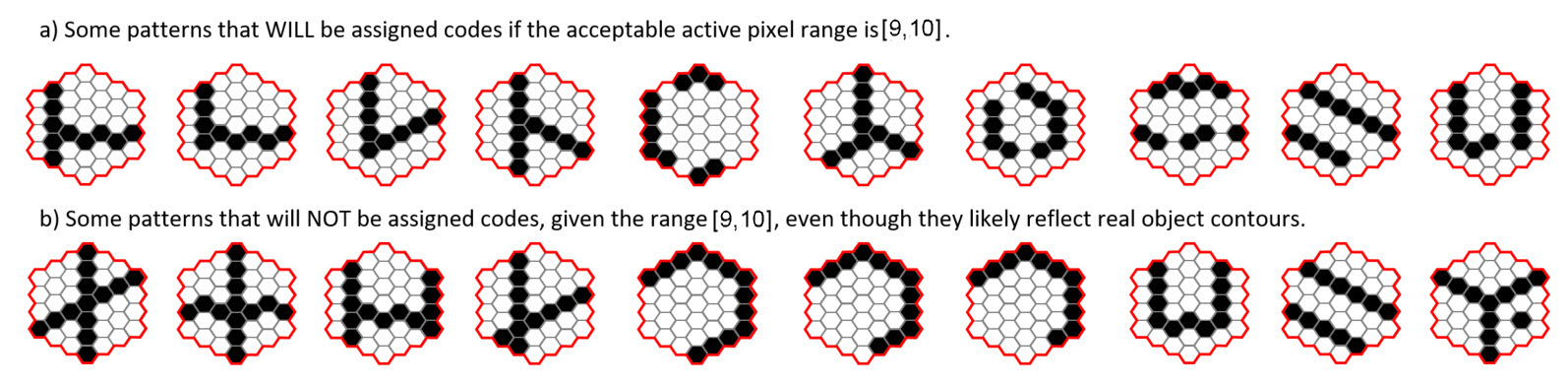
Figure 3: Possible input patterns (features), assuming the described preprocessing, for a hexagonal RF of about 37 pixels. (a) If the allowable pixel activation range is [9,10], these inputs will activate the mac and be assigned to a code. (b) These inputs will not be assigned since they are outside the allowable range. This, despite the fact that they are most likely due to structural regularities in the input domain. One might counter that it seems like a bad idea to summarily not create a code for an input that reflects a structural regularity. While this is generally true, it is partially mitigated by the fact that a typical macroscopic object/event will span a large number of such small-scale RFs. Thus, it may not be particularly deleterious to fail to encode a fraction of such instances.

Nevertheless, for biologically realistic instantiations of a mac, e.g., Q=70, K=20, likely at most only a few thousand codes could be safely stored. [This estimate is based on roughly extrapolating from these capacity results in which a model with Q=100, K=40, and a 10x10-pixel input level, was able to store, to 97% recall accuracy, 3,084 10-frame sequences (equivalent to 30,840 individual frames). We would expect lower capacity in the realistic case due to the lower Q and K values and the need to map similar inputs to similar codes (which was not imposed in the hyperlinked studies).] Thus, as the eye experiences the world (and again, assuming stages up to and including the thalamus perform the described preprocessing), it is likely that the number of unique inputs this mac experiences, will quickly exceed its capacity. Therefore, to prevent this mac from losing memories, we will have to freeze it before it exceeds that capacity. In practice, the freezing is implemented simply by preventing any further changes to the weights comprising the mac's bottom-up afferent weight matrix: this effectively prevents new codes from being stored.

We must now consider the consequences of freezing a mac. We will refer to the set of codes stored in the mac, or rather their corresponding inputs, as the mac's basis. Note that although we call this set of stored codes (experienced features) a basis, the following must be understood. In the typical machine learning concept of a basis, a novel input, X, is represented by a linear superposition of multiple, perhaps 100's, of basis elements, and we can measure how closely that linear superposition approximates X. This view remains sensible regardless of how overcomplete the basis is (even though as overcompleteness increases, the expected number of basis elements needed to achieve any given overall average closeness over all inputs, necessarily decreases). In contrast, in our model, once a mac's basis is frozen, only those codes (basis elements) that have been stored can become active and only one of those codes will become active in response to any future novel input. If the mac was frozen before reaching its capacity, then, with high expectation, the code that becomes active will be the code of the input that most closely matches X. Thus, it is not the case that independent codes of multiple basis elements are co-activated and collectively represent X, but rather that a single basis element is activated to represent X. With this understanding in mind, we consider the consequences of freezing a mac's basis in terms of two questions.

1. First, given the assumptions above, i.e., the preprocessing, the tight range of input activation required to activate the mac, and the naturalistic input domain, how good a job can the frozen basis do at representing all future inputs to the mac? More formally, we define the fidelity of a basis to be the expected intersection of the mac's input pattern to the nearest basis element, averaged over all future inputs for which the mac activates. Given all the assumptions of this example, we expect that a basis of only a few thousand, or even a few hundred, could yield quite high fidelity, approaching 100%. One of our near-term goals is to empirically verify this claim.
2. Second, given that an L1 mac corresponds to only a small portion of the whole visual field and thus, that its input pattern may correspond to only a small portion of an object or scene to be recognized, how high a fidelity is really required for any single L1 mac? This concept is illustrated in Figure 4. Broadly, the idea is simply that the object of interest here, the plane, spans many macs' RFs. The overall shape of the plane, i.e., the relative position of its wings, nose, tail, etc., is carried not by the precise features active in each RF, but by the relative positions of the RFs themselves. This information, i.e., the overall pattern of active L1 macs, can, in principle, be recognized by an L2 mac whose RF included all the L1 macs shown. Thus, to the extent that some of the meaning of an overall input image is carried by the spatial topology of the macs at a level, J, this reduces the fidelity needed by the level J macs in order for the level J+1 macs to achieve any given level of fidelity. Figure 4b shows the case where the closest-matching basis element to the actual contour (red in panel a) is activated. Figure 4d shows that even if very poorly matching basis elements are activated in many/all of the apertures, substantial information, e.g., that the object has four lobes is still present. Figure 5 provides additional intuition as to why a lower fidelity at a small spatial scale might be sufficient to support higher fidelity at higher levels. Again, we intend to empirically analyze this principle in the near future.


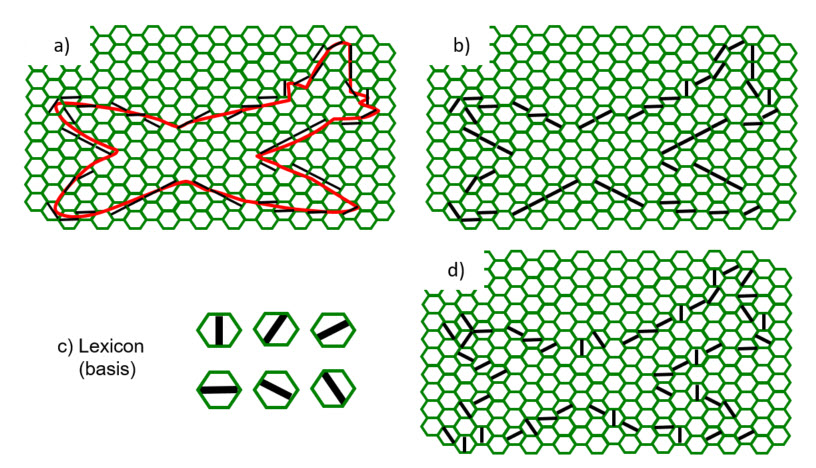
Figure 4: Illustration that in a hierarchy, some information can be carried by the topology, i.e., where features occur in the global input space, which reduces the amount of information, e.g., fidelity, needed in individual portions of the global space.

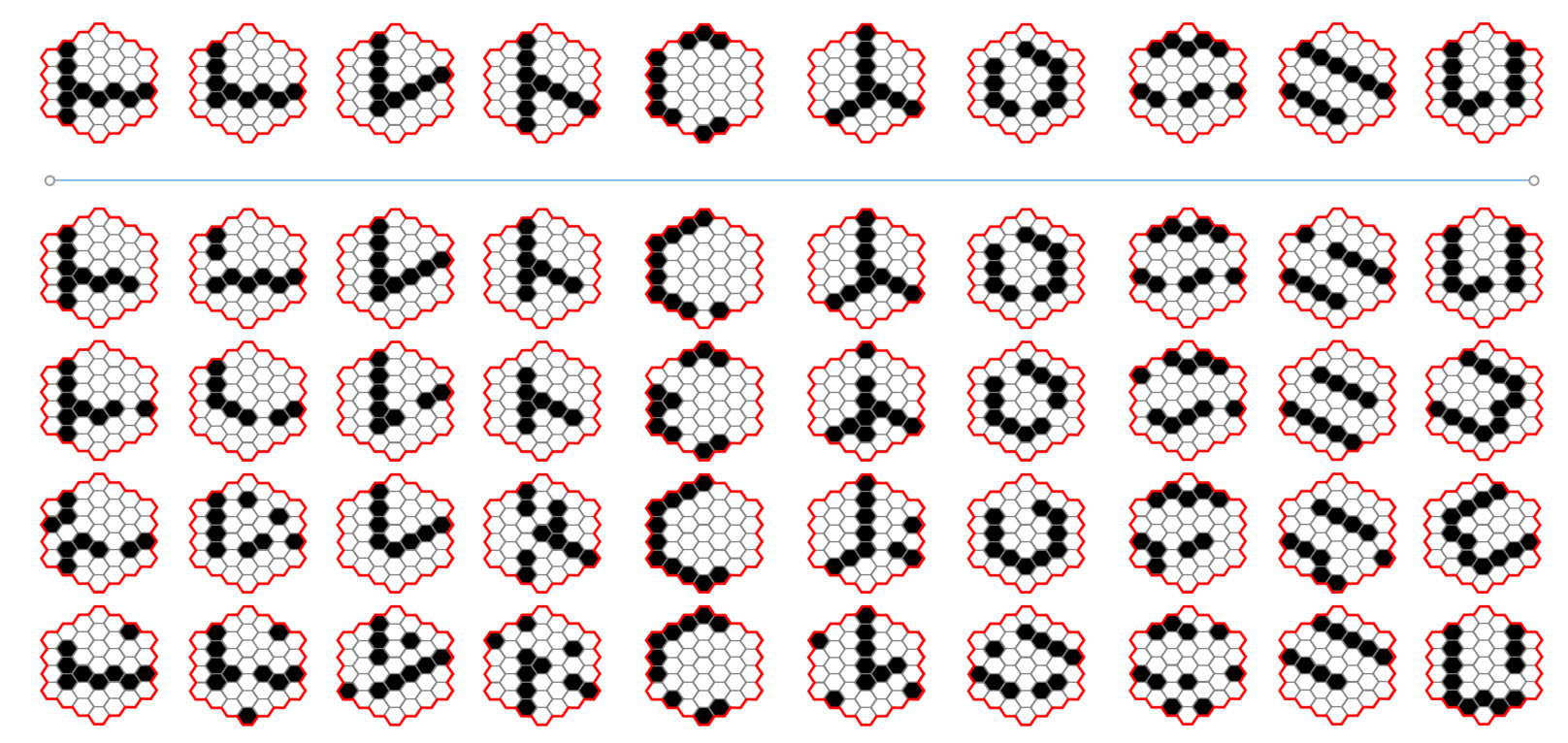
Figure 5: Illustration of why a lower fidelity at a small spatial scale might be sufficient to support higher fidelity at higher levels. The question here is: wouldn't the pattern above the blue line be a sufficiently close representative of any of the patterns below it in its column, in terms of registering the presence of a small-scale part of a larger whole.? It is quite plausible that if each of the patterns below the blue line caused the SDR code of the pattern at the top of its column to activate, thus computing a local invariance, a class judgement process occurring at a higher level might still have high accuracy.

Overall, these considerations suggest that freezing learning in lower level macs, e.g., in V1, V2, may be quite acceptable: it permanently preserves the learning in these macs (i.e., protects against catastrophic forgetting), yet allows that the frozen bases might yield sufficiently high fidelity for representing all future inputs to the system.

Now, we consider the higher level macs.  First, it is essential that any autonomous, intelligent system be able to store new information, i.e., new permanent memory traces, for its entire lifetime, cf. "lifelong learning".  As discussed above, we will be satisfied with a statistical argument that the rate at which new inputs are expected to occur to macs at level J decreases exponentially with J. Thus, broadly, the envisioned scenario is that as the system experiences the world, many/all of the macs at lower levels may reach capacity and be frozen rather early in the system's lifetime, but that due to the statistical argument below, many/some of the macs at higher levels will never reach capacity, and thus never be frozen, and thus be able to store new inputs throughout the expected lifetime of the system. I emphasize that there is substantial evidence, across many/all sensority modalites, for "critical periods", i.e., the phenomenon that if a particular cortical region does not experience certain classes of input prior to some age, that region never develops the ability to recognize such inputs.  I believe that the purpose of biological critical periods is precisely to serve the functionality described here, i.e., prevent too many codes from being stored in macrocolumns, and thus prevent catastrophic forgetting. Furthermore, there is plentiful anecdotal evidence that as we age, the features/concepts with which we experience, intrepret, deal with, the world become entrenched.  In general, over many decades, one retains to ability to form new higher level concepts (abstractions), but, to a large extent, they are built out of long-fixed low-level features/concepts.

So, by what reasoning can we claim that the rate at which macs at higher levels approach capacity likely slows down exponentially with level? First, as described above, the particular preprocessing used and the tight criteria for activating a mac already greatly constrain the set of inputs expected to be experienced and stored in a mac. Suppose that we impose that following the point of freezing, not only will no new codes ever be stored (learned) in the mac, but also that only the set of already stored codes will ever be allowed to activate in the mac.  Now, suppose that the RF of a level J+1 mac is a set of level J macs.  That is, the boundary of the level J+1 mac follows exactly the boundary of the set of level J macs comprising its RF. That means that following the point at which all level J macs freeze, the set possible of inputs to a level J+1 mac that can ever possibly occur is fixed.  Suppose also that a level J+1 mac only activates if the number of active level J macs in its RF is within a tight range. For concreteness, suppose an L2 mac's RF consists of 9 L1 macs and that the L2 mac will ony activate if exactly three of its nine L1 macs is active, i.e., if the number of active L1 macs is in the range [3,3].  Thus, the space of all possible inputs to the L2 mac can be partitioned into sets corresponding to C(9,3)=84 3-part compositions. Suppose that L1's critical period has elapsed (though, the freezing actually occurs on a mac-by-mac basis) and that the basis size of all the frozen L1 macs is 1000. In this case, the total number of actual input patterns that the L2 mac can ever experience for the remainder of the system's life is 84x1000x1000x1000 = 84x10⁹. This may seem like a large space, but we must compare it to the total number of unique L0 input patterns that were initially possible, i.e., prior to any learning at any level, within the "composite L1 RFs" corresponding to the 84 specific 3-part compositions. Let's consider just one of those 84 3-part compositions. We said above that the space of possible patterns that would cause any of the L1 macs to activate was C(37,9) + C(37,10) (~473 million). However, due to the filtering, we speculated that only perhaps a few tens/hundreds of thousand patterns, let's say 10⁵, for concreteness, would actually ever arise in the RF of any given L1 mac. Thus, the total unique patterns for a single 3-part composition is 10¹⁵, and the total for all 84 3-part compostions is 84x10¹⁵. Thus, the effect of the critical period has been to reduce the input space to the L2 mac by 6 orders of magnitude.

The above reasoning applies at every level. In general, we could quantify the reduction in input space at level J+1 post freezing of level J macs, but the broad conclusion is that the combined effect of hierarchy, compositional RFs, and critical periods, reduces the space of possible inputs to a level J mac exponentially relative to its initial size, i.e., prior to any learning. Note that in Sparsey, all weights are zero at "birth".  Further, the size of that relative reduction increases exponentially with level.

However, our ultimate goal (Point 2, above) is to show that the expected rate at which new inputs occur decreases exponentially with level. If that is true, then the higher levels of a model with only a small number of (e.g., <10) levels could have very low expected rates of occurrence of new features.  Such a model would therefore have a very long expected lifetime operating in a natural world without exhausting its memory capacity. Broadly, the intution that supports this is that natural worlds have 1/f statistics, i.e., the expected frequency of input patterns, i.e., features, decreases at least linearly with the size/complexity of the features. This reflects the strongly, hierarchical, recursive, compositional structure of the natural world, both in space and time, i.e., entities are made of parts, which are made of smaller parts, etc. The forces/relations that exist between parts at the same scale and across scales severely limits the configuration spaces of wholes (and intermediate compositions) and therefore the possible appearances of wholes. What this essentially means is that only a relatively tiny fraction of the space of all possible inputs can actually occur, but those that do occur tend to recur far more frequently than chance, i.e., a "heavy tail". If a relatively small set of input patterns occur far more frequently than chance, that implies that the rate at which new patterns occur must be much lower than chance. And, note that a novel input, X, is assigned a code only on its first occurrence: all subsequent occurrences of X simply reactivate its previously assigned code, i.e., X is recognized. Moreover, the sensitivity of a mac's match computation (i.e., the computation of the familarity of a new input given the set of previously stored inputs) can be parametrically varied.  In general, there will be hypersphere around X within which a novel input, X', will, with high probability, cause X's code to reactivate exactly.  This acts to further reduce the effective rate at which new codes are assigned, i.e., the rate at which the mac approaches its storage capacity.

Sparsey has one further principle that further reduces the rate at which a mac adds new codes. It is the principle that the number of time steps that a code stays active, i.e., its persistence, increases with level.  In almost all studies to date, we have simply doubled persistence with level. This explicitly halves the rate at which new codes are assigned at each higher level and acts on top of the statistical principles described above.

While not a proof, I believe the above principles collectively support the claim that the expected rate of occurrence of new inputs drops exponentially with level and therefore that we can expect hierarchies of macs to have long operational lifetimes in natural worlds without ever exhausting memory capacity. Empirically verifying and quantifying this property is a high priority task for the near future.  As part of this analysis I will also compute fidelity measures for each level. That is, in addition to the requirement that the overall model retains the ability to learn new permanent memory traces throughout its life, it must also be the case that the model builds an internal model that captures the domain's underlying statistics and thus does well at recognizing new instances and making predictions.  Given that the algorithm that runs in each mac, for both learning and best-match retrieval, has a fixed number of operations for the life of the system, and that an instance of either learning or retrieval for the whole model involves a single iteration over the macs comprising the hierarchy, the time complexity of learning and best-match retrieval for the whole model is also fixed for the life of the system, and thus, effectively O(1).