Overlapping Mac Receptive Fields (RFs)
Figure 1 illustrates overlapping bottom-up RFs (URFs) in a Sparsey model. Panel a shows the URFs (cyan patches) of L1 macs, 7, 8, 14, and 15, the last two of which overlap (as was also shown on the hyperessay's start page, Figure 3). The L1 URFs consist of varying amounts of pixels. On the frame depicted, macs 14 and 15 each have four active pixels in their URFs (the exact URF boundaries are hard to see here), which satisfies their respective criteria for activating. Mac 7 also meets its activation criteria with five active pixels. Mac 8 has six active pixels which does not meet its activation criteria (and so is not shaded rose and the pixels in its URF are gray). Panel b shows that the URF of L2 mac 3 subsumes those of L1 macs 14 and 15. L2 mac 3's immediate URF consists of the six L1 macs shaded either cyan or purple. Its activation criteria is in terms of the number of active macs in its immediate URF, which we can all its L1-URF, rather than in terms of the number of active pixels in its input-level URF, which we can all its L0-URF. In this case, L2 mac 3's criteria is that exactly two of the L1 macs in its URF are active. The idea here is to impose a sort of discrete compositionality constraint: that is, a higher level mac, such as L2 mac 3, should become active if the portion of the input falling within its L0-URF (the large, subsuming cyan patch at L0) has two "parts". So, first of all, that means that there are C(6,2) ("6 choose 2") = 15 way of choosing exactly two active L1 macs within L2 mac 3's L1-URF. Thus, there are 15 configurational (i.e., topological / geometric) classes into which all specific pixel activation patterns that occur in L2 mac 3's L0-URF will fall. But over the course of learning, each of the six L1 macs will store a set of inputs (that occur in their respective URFs), i.e., a basis. Assuming, for simplicity, that each of the six L1 macs stores exactly 100 inputs (basis elements, or features) and is frozen, and assuming that all future inputs falling within any one of those L1 URFs will activate the closest-matching stored input, then exactly 15 x 100 x100 = 150,000 unique inputs will every possibly occur in L2 mac 3's L1-URF for the rest of the model's life. Note however, that most of those will never occur. More importantly, assuming biologically realistic parameters, it is unlikely that any one macrocolumn would be able to reliably store more than a few hundred to a few thousand codes. So although 150,000 unique inputs might occur in L2 mac 3's L1-URF, only a small subset of them, let's say 1,000, will be assigned to permanent SDC codes:, i.e., L2 mac 3 will ultimatley have a basis of 1,000 features, where each of those features is composed of two smaller-scale features, which may in fact overlap at the pixel level, but which have some spatial separation. This same scheme applies up through all the levels of the hierarchy, i.e., higher level "wholes" are composed of "parts", which are composed of "sub-parts", etc.
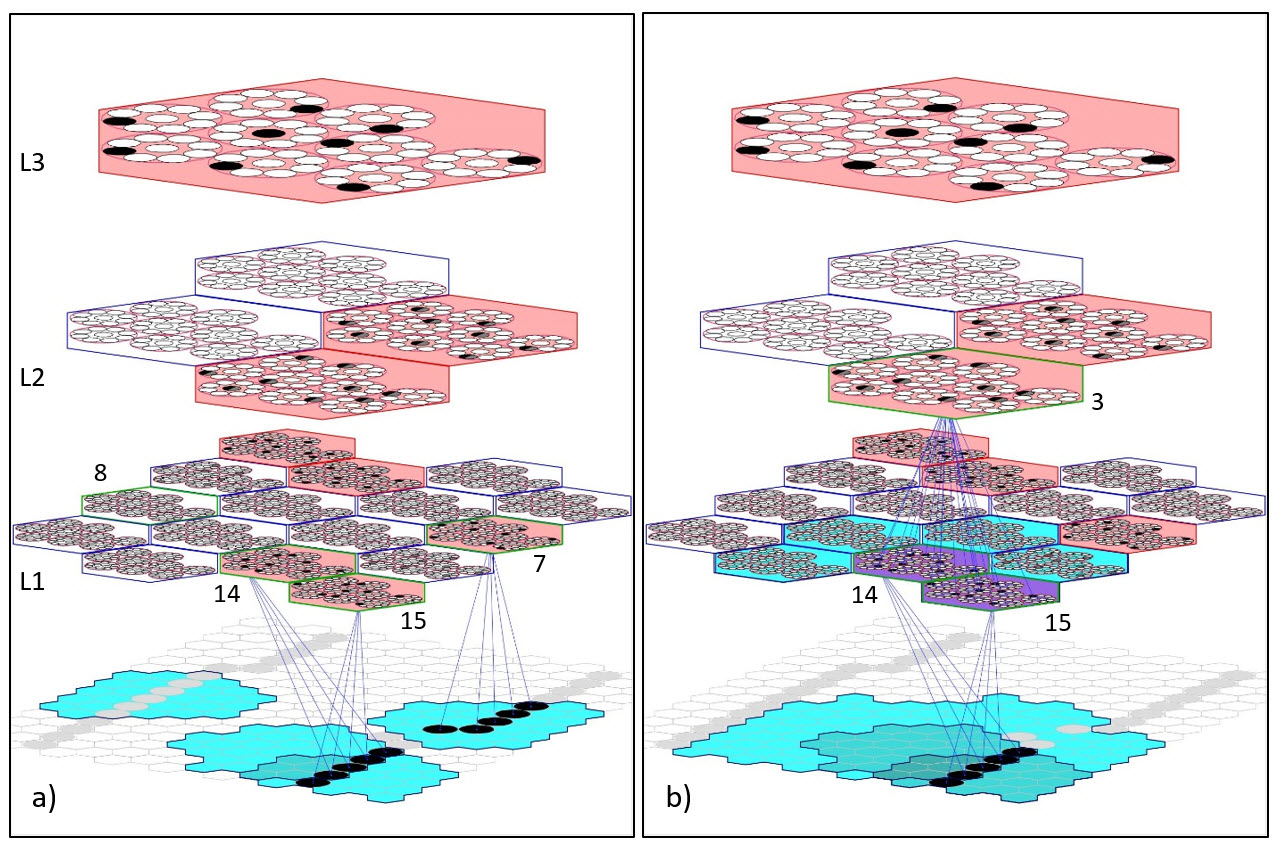
Figure 1: Illustration of overlapping URFs of Sparsey macs. See text for discussion.
We make the following observations about Fig. 1.
- Almost the exact same set of active pixels activates both macs 14 and 15 in this instance (see Figure 3 on the hyperessay start page for clarification if needed). For mac 14, these pixels constitute a vertical edge feature on the right edge of its URF and for mac 15, they constitute a vertical edge in the center of its URF. Thus, there is clearly redundancy here; each of the intersecting pixels is represented twice at level L1, as part of the feature encoded by the sparse distributed code (SDC) that becomes active in mac 14 and as part of the feature encoded by the SDC that becomes active in mac 15. Both of these L1 SDCs become associated with the single SDC in L2 mac 3. Thus, essentially the same visible edge in the input space—i.e., the same information—is encoded redundantly and via different hierarchical routes in L2 mac 3's SDC. However, with respect to the individual macs, 14 and 15, the features have different semantics, i.e., a vertical edge at the right of and at center of the URF, respectively. It's only in conjunction with the different topological semantics that L1 macs 14 and 15 have with respect to L2 mac 3, that the feature encoded by macs 14 and 15 can be considered redundant. Note that there are benefits of this redundancy: a) if either mac 14 or 15 dies/malfunctions, the edge feature is still represented the L2 level; and b) this redundancy is essentially an instance of overcompleteness and, in general, the more overcomplete a basis is, the easier it is (fewer samples needed) to learn.
- The input "units" comprising L2 mac 3's URF are themselves macs (the six cyan or purple macs in Figure 1b). Thus, whenever L2 mac 3 activates it will be because an acceptable number of its six afferent L1 macs are active. The code active in each such L1 mac will represent some particular input feature (but see point 3 below). Thus, the code active in L2 mac 3 formally represents a composition of features, which, as in Figure 1, can overlap. Thus, there is a meta-level of overcompleteness operative in the model, the first level being the overcompleteness that may be present in the set of features learned (and stored) in any individual mac.
- Above, we speak of an SDC active in a mac as representing a particular feature. However, all codes stored in a mac are stored in superposition. Thus, formally, whenever any single SDC is active, that SDC can also be viewed as a (similarity or likelihood) disribution over all the codes stored in the mac.
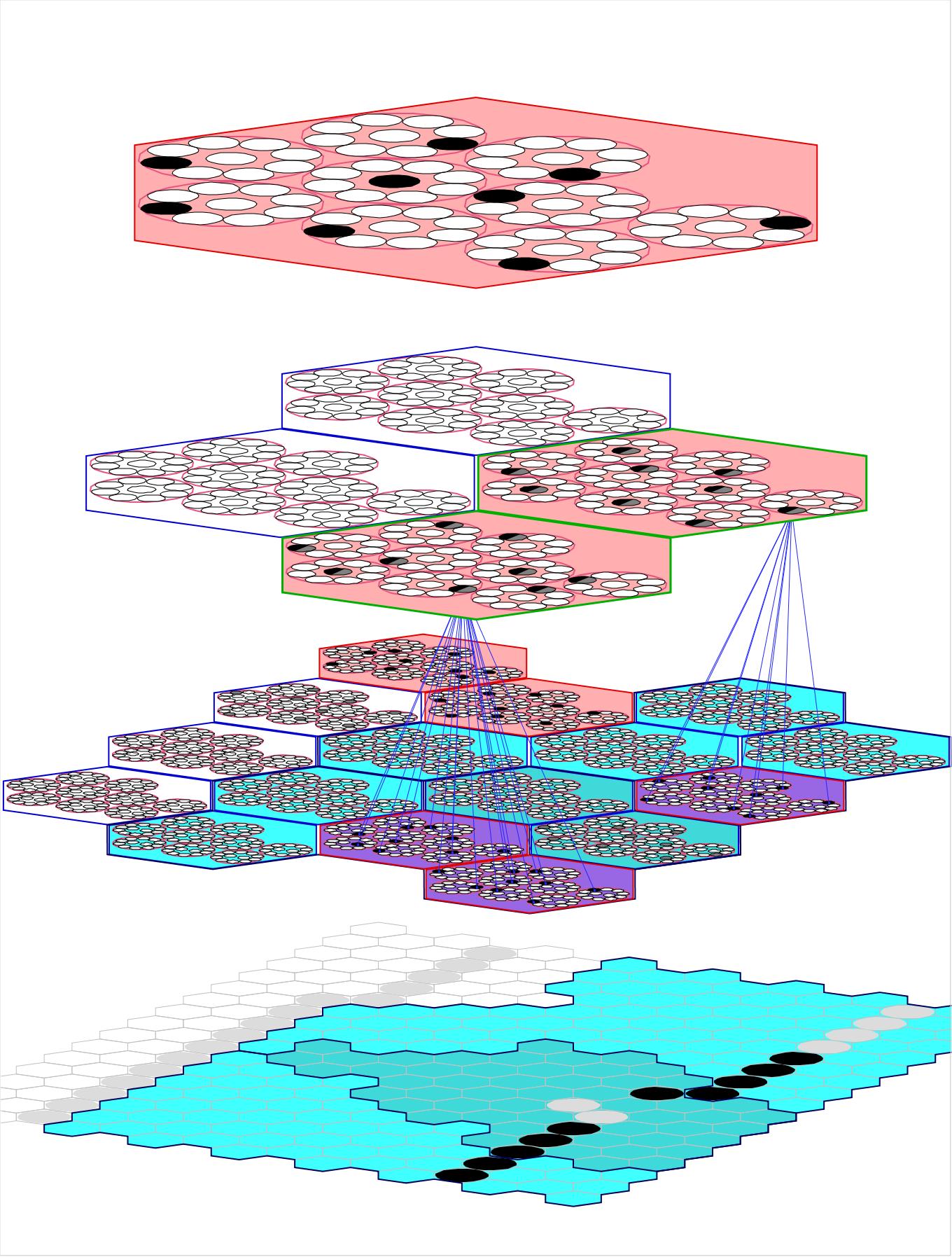
Figure 2: The URFs, both immediate (at L1) and at the input level, of L2 macs 1 and 3 shown. The light gray pixels are ones that, though active, are not represented, i.e., do not influence the choice of codes, at L2 because they do not fall within the URF of an active L1 mac. A crucial reason for and benefit of overlapping URFs is to minimize the number of active pixels (more generally, input features) that fail to be encoded at higher levels.
The points made on this page barely scratch the surface of all the possibilities / consequences of overlapping RFs, compositionality, and how the cortex learns to "disentangle" (cf. Cox and DiCarlo) the structure present in the input space.
