This page describes a recent simulation experiment performed as part of our seedling research under DARPA's UPSIDE program. The experiment involved single presentations of each of the five 64x64 snippets, from 36 to 76 frames long, (one is here) to an 8-level 3,261-macrocolumn Sparsey network, with ~75 million synapses.
The simulated macs are small compared to their proposed cortical analogs. Real cortical macs have about Q=70 minicolumns, each with about K=20 L2/3 pyramidal neurons (principal cells); in this model, Q=7 for macs at all cortical levels and the K values for levels for V1 to Prefrontal were, 7, 7, 7, 9, 10, 12, 14, respectively.
The animation shows (a tiny fraction of) the network processing during all 36 frames of a recognition test run for a snippet in which the actor's leg is bending (as part of a Kick action) (taken from the ViHASi data). Blue / green / magenta lines represent bottom-up (U), horizontal (H), and top-down (D) signals, respectively. Active macs are shaded and outlined red. V1 and V2 macs are too small to see at this scale. The minicolumns and neurons are not shown here, but when a mac is active, that means that a sparse distributed code (SDC) (or cell assembly, or ensemble) consisting of Q co-active neurons is active. We emphasize that Sparsey's SDCs turn on and off as wholes during both learning and recognition (retrieval). This is consistent with the increasing awareness in neuroscience that it is whole sets of co-active neurons that represent features/concepts, not single cells (cf. Yuste, Olshausen, Buszaki, and others).
The algorithm underlying this simulation, Sparsey's Code Selection Algorithm (CSA), executes in every V1 mac (that has sufficient bottom-up input) on every frame. It executes in every higher level mac as well, but code activation duration, or persistence, increases with level, e.g., V2 and V4 codes persist for two frames, PIT codes for four frames, etc. This results in sequences of codes in lower level macs becoming associated (via learning in the U and D synaptic (weight) matrices) with single codes (or shorter sequences of codes) in higher level macs, i.e., hierarchical temporal nesting, which in conjunction with the hierarchical spatial nesting due to cumulative fan-in/out across levels, provides a robust and flexible basis for learning hierarchical spatiotemporal compositional (cf. recursive part-whole) representations of actions/events, and higher-level conceptual/abstract entities.
The CSA computes, for each of the QxK principal cells comprising a mac, normalized versions of the U, H, and D input to the cell and multiplies them, producing a normalized (between 0 and 1) measure, V, which constitutes a local (to that cell) measure of the evidence that that cell should become active (we could also refer to this as its local support, or likelihood, or implication).
What sets Sparsey apart from other models is that CSA does not simply activate the cell with the max V in each of the mac's Q minicolumns. Rather, it first computes a global (to the mac) measure, G, of the evidence for the maximally-implicated whole mac code, i.e., for the set of Q cells that have the max V in their respective minicolumns; specifically, G is just the average of Q max V's. The CSA then injects an amount of noise/randomness into the final selection of winners that is inversely proportional to G. This simple procedure is what confers Sparsey's property that more similar inputs (to any given mac) are mapped to more similar (more overlapping) SDCs, the "SISC" property.
If you think about it, you realize that G can only be 1 when there is at least one cell in each minicolumn with V=1. And, you can only have a cell with V=1 if that cell's receptive field (RF) tuning matches its current total (i.e., including its U, H, and D) input. But that can happen only if that cell was chosen to represent that total input on a prior occasion (i.e., on a learning trial). Actually, that can also happen when too many SDCs have been stored in a mac, so we need to ensure that macs do not attempt to store too many SDCs during learning (hence "critical periods"). But, assuming we are in a regime in which not too many SDCs have been stored (i.e., a "low-crosstalk" regime), then if G=1, that can only mean that this mac has experienced the current total input on a prior occasion. In this case, we want, with very high probability, to pick the cells with max V in their respective minicolumns to be the mac's SDC. Thus, when G is near 1, we want to add little to no noise/randomness into the winner selection process. On the other hand, if G is low or close to zero, that can only happen if the mac has not previously experienced its current total input. But in that case, we want to pick an SDC that has little intersection with any previously stored SDC. In this case, we want to add more noise into the winner selection process. The details of how G is used to transform the probability distributions (within the minicolumns) from which the Q winners are chosen can be found in Dr. Rinkus's publications.
As the table below shows, in this experiment, the model was able to reinstate almost the entire traces at levels PIT and higher across all frames of all five snippets (a total of 252 frames). Although the individual neurons are not shown in the animation above, one can see that even in this single 36-frame trace, the total number of mac activations that occur in levels PIT and higher is in the hundreds, thus the total number of cell activations (just in levels PIT and higher) is in the thousands. The average accuracy of the traces across all 252 frames for the lower levels were: V1=57%, V2=85%, and V4=90%. If we include V2 and V4, the number of cell activations underlying these traces is in the tens of thousands and they are reinstated virtually perfectly (albeit ~85% at V2).
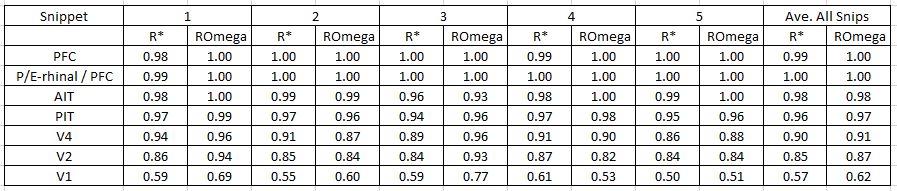
But we can see another key phenomenon in these numbers. Specifically, we see that the recognition accuracy at V1 is poor, ~57%, and more generally, that accuracy increases with level. This seems counter intuitive because one might think that if codes begin to go wrong at the lowest cortical level, then they surely must get worse, i.e., compound, at higher levels. However, this clearly does not happen. Essentially, Sparsey's macs implement a kind of associative clean-up memory with every new code chosen. We will be analyzing this and explaining it in detail in subsequent work.
