The video below illustrates the novel principles by which Sparsey's code selection algorithm (CSA), originally described in my 1996 thesis, and improved versions in several pubs since, e.g., Rinkus (2010), Rinkus (2014), and Rinkus (2017), causes similar inputs to be mapped to similar codes (SISC), where the similarity metric may generally be spatiotemporal and/or multimodal.  The first principle is that the codes are sparse distributed codes (SDCs), a.k.a. sparse distributed representations (SDRs), a particular kind of Hebbian cell assemblies (CA).  In Sparsey, an SDC coding field is a set of Q WTA competitive modules (CMs), each with K binary units.  Thus a code is a set of Q units, one per CM.  So all codes are of the same size, Q. In this case, the natural similarity metric for SDC is size of intersection (there is no need to normalize by the union, i.e., no need for Jaccard).  Given this reprsesentational format, SISC can be achieved simply by making the level of noise in the code choice process vary inversely with the familiarity (directly with the novelty) of the input.  This video and discussion and the corresponding DOWNLOADABLE APP explain this in more detail.  The app allows the user to play with parameters and understand the computationally simple means by which Sparsey achieves SISC. To run the app, download the jar file and double-click it. If you have java installed on your system it should work. It'll probably pop up a warning that the jar is an executable and to be careful, but it's safe.         

The idea that similar inputs should be mapped to simlar codes is uncontentious.  However what makes Sparsey unique is that its learning algorithm creates new codes, adhering to SISC, in fixed time, i.e., with a number of operations that remains constant as the number of stored items grows.  Furthermore, the fact that similarity is preserved during learning means that the most similar stored input can also be retrieved in fixed time!   Sparsey is thus a direct alternative to locality preserving hashing (LPH) and to locality sensitive hashing (LSH).

In fact, Sparsey:

• is conceptually and implementationally simpler than exisiting descriptions/implmentations of LPH and LSH.
• is representationally richer than LSH: Sparsey captures arbitrarily graded degrees of similarity, whereas LSH theory is based on distinguishing close vs. far (a binary distinction).
• applies equally well to both spatial and spatiotemporal (sequence) domains.
• learns the similarity metric (the hash) directly from the data, based on single-trial, on-line, non-optimization-based learning.
• is biologically plausible (as described in Rinkus (2010) and Rinkus (2014)).

In the video, the coding field ("mac", short for "macrocolumn", which is a structural/functional structure of which neocortex is composed) is shown in the figure at bottom of the video and its state is described in detail in the middle right panel (entitled "Mac comprised..."). The figure at left bottom of video is a depiction of the mac: it is comprised of Q=10 winner-take-all (WTA) competitive modules (CMs), each with K=5 binary units. The input field of 20 binary units is completely (all-to-all) connected to the mac with binary weights. This all-to-all connectivity is an essential property of the model. The blue lines just emphasize the complete matrix from the input field to one of the CMs. Although we depict this underlying architecture for the model being simulated in this video (and the associated app), the app does not explicitly model (i.e., generate and present) inputs. Rather, when an input item is effectively presented (which can be caused in several different ways), it will have a familiarity (inverse novelty) that is impliclty defined by the setting of the "Max V in each CM" slider. And, the effects of a notional set of previously learned inputs are implicitly defined by the settings of the crosstalk sliders (at top of video) (desribed precisely below). The middle right panel shows two variables, V and ρ, for every unit in the mac. A unit's V value represents its normalized [to (0,1)] input summation from a notional input item, i.e., a notional set of active binary features in the input field. We can depict such a normalized input because we assume that all inputs that arise in the input field will have the same number of active features, say, 7, out of the 20. A unit's ρ value is the final probability of choosing it as winner in its respective CM. Actually, the CSA first produces an intermediate vector of values, the relative probabilities of winning (μ), which are then re-normalized to the vector of final probabilities (ρ). This is done independently for each CM. Specifically, a unit's μ value is produced by mapping its V value through the V-to-μ transform (shown at upper left), which is formally a sigmoid. The sliders allow the user to vary three parameters of the sigmoid, its overall height, governed by the V-to-μ Range Mult" slider, its eccentricity (controlled by the "Inverse Sigmoid Eccentricity" slider, and the horizaontal location of its inflection point. In the full Sparsey model, the familiarity measure, G, controls the height of the sigmoid: as G drops to 0 (a completely unfamiliar, i.e., novel, input), the sigmoid height drops to 0, i.e., the V-to-μ transform becomes the constant function, thus causing all units in a CM to end up being equally likely to win. However, in the app, G does not control sigmoid height. Rather the user is free to investigate the properties/capabilities of various causal relations from G to any of the V-to-μ transforms three parameters. CM 1 has a yellow background to indicate that the V-to-µ plot (upper left) and "single CM" panel (middle left) are showing the details of CM 1.  The user can click on any of the CMs in the middle right panel and it will be shaded yellow and its data will be shown in the other two plots.

The overall idea of the app is that the user can see how the familiarity, G, of a notional input, statistically determines the size of the intersection the code assigned to it with the code of the notional closest matching stored input. As stated above, the app does not actually explicitly simulate (generate) inputs.  Rather, it explicitly generates a V distribution, across all the mac's units, that reflects: a) a given degree of familiarity (i.e., by the having a particular average max V value across the Q CMs; and b) a given level of crosstalk, which indirectly reflects a set of previously learned (stored) inputs. It generates such a vector of V values each time the user presses the "Generate new sample" button. It also generates such a vector each time the user clicks on any of the four "Phase of life butons" (the behavior for the phase of life buttions is described in more detail below). Given that Sparsey's learning law states that whenever a synapse experiences a pre-post coincidence, its weight is permanently set to 1, we can simulate the presentation of 100% familiar input by generating a V vector that has at least one unit with V=1 in each of the Q=10 CMs (again, because familiarity, G, is defined as the average max V value across all Q CMs). Strictly, this is true if we are also assuming that the total number of inputs stored thus far is small enough so that the crosstalk interference between them is low enough so that the probability of units spuriously having (i.e., due to the crosstalk) V=1 is low. Similarly, we can simulate presentation of an input with 50% familiarity, by generating a V vector such that the max V value in each CM is 0.5, and so forth.

The V distribution, in each and every CM, is generated as follows.

1. One cell is randomly chosen to have the max V value, which is the current value of the "Max V" (or equivalently, "G") slider. At the start of the video (and when the user opens the app), the slider is set to V=1. As described in the prior paragraph, this corresponds to a case where we're simulating an input that is 100% familiar. But the user should experiment with this slider.
2. The V values of the other K-1 cells in the CM are drawn uniformly from the crosstalk range, determined by the the min and max sliders at upper right, which are set 10% and 20% at the start of this video.  Indeed, the crosstalk parameters impose further implicit constraints on the history of inputs, i.e., higher average crosstalk implies more inputs have been experienced.

Above each CM's V distribution, is its ρ distribution. Sparsey chooses/selects/activates a code in a mac by choosing one cell from the ρ distribution in each CM.

You can see that some of the ρ bars are red. That indicates an error: i.e., a CM in which the cell with highest V was not ultimately chosen by the draw from the ρ distribution. Why do we consider this an error? Because, when G=1, that means there must be at least one cell in each CM that has V=1. And, for a cell to have V=1 means that all active input features comprising the current input have, on some previous occasion (i.e., for some previous input), had their synaptic weights onto the cell increased because, on that occasion, the cell was activated as part of the code chosen to represent that prior input. So, assuming that the mac is in the regime in which not too many codes have been stored (i.e., crosstalk is low), the fact that there is at least one cell in each of the Q CMs that has V=1 strongly indicates that that set of Q cells (assuming there is exactly one cell with V=1 in each CM) was activated, as a whole, on a prior instance in which the current input also occurred. In other words, when a) G=1, and b) not too many codes have been stored, the input is highly likely to be a repeat of a prior input, i.e., to be completely familiar, in which case we want the same set of Q cells that was chosen and activated in response to that prior instance to again activate. Thus, when conditions a and b hold, if a cell is chosen in a CM that is not part of that set of Q cells, i.e., of the code (memory trace) of that prior, familiar, input, then we can consider that cell to be an error.

With the above in mind, when "Max V" is set to 1, the "Actual Accuracy" field reports the fraction of the Q CMs in which the correct cell, i.e., the cell with highest V, wins. Note that we can consider the probabilistic choice process in each CM to be a Bernoulli trial, where success probability is just the ρ value of the max-V cell, which we can call the max-ρ value, and the failure probability (i.e., any other cell in the CM being chosen) is 1 - max-ρ. Thus, the "Expected Accuracy" field reports the average of the Q max ρ values.

But now consider the situation when we lower the "Max V" slider. A lower max V means that the current input has not been seen exactly before. Again, assuming the regime where not too many codes have been stored in the mac, if the max V is 0.5, that implies that the current input has about half of its features in common with the closest-matching previously stored input. A max V of 0.75 means that the current input has about 75% of its features in common with the closest-matching stored input, etc. So, in order to enforce SISC, i.e., preserve similarity from the input space into the code space, what we want is that as we lower the "Max V" slider, while keeping the max and min crosstalk limits constant, we lower the Expected Accuracy. That is, as max V decreases, we want the probability of picking the max-ρ (which is also the max-V cell) in each CM to also decrease. This has the effect of decreasing the expected intersection of the code assigned to the current input with code of the most closely-matching stored input. So in this case, i.e., when G < 1, the red bars shouldn't be construed as errors, but rather, thinking of the implied input item as the presentation of a novel item on a learning trial, these cells corresponding to red bars show the CSA appropriately picking a code with progressively lower (i.e., for progressively lower G values) intersections with the codes of the (implied) closest-matchign previously stored items. The full Sparsey model, reduces the probability of choosing the max-ρ cell by squashing the V-to-μ transform as G drops. But in the app (and the video), the falttening of the ρ distributions in the CMs is just do to the fact that the max V (thus ρ) in each CM is dropping towards the upper limit of the crosstalk value. The squashing of the sigmoid in the full model (or manipulations of the sigmoid's other parameters) has the effect of flattening the ρ distributions, which can be viewed as increasing the amount of noise in the individual choices (i.e., in each of the Q CMs) and thus, in the selection of the overall code.

So, with the above in mind, if you now watch the video, what you see is that as the "Max V" slider is lowered smoothly (you can see the black bars in the V plots of all the CMs in the Mac panel drop together), the "Expected Accuracy", i.e., the expected intersection with the closest-matching stored code, decreases smoothly. This, in and of itself, constitutes a demonstration of SISC. Note that as you decrease the max V you will also see the number of red ρ bars increase. (Actually, each time the "Max V" slider moves a little bit, a new draw is made. That's why you see red bars updating quite a bit. To make this clearer, you might want to put the cursor somwhere on the Max V slider and just do successive clicks; each click will change the max V value slightly and generate a new sample.) If you download the app, you can experiment with the various parameters (eccentricity, range multiplier, and inflection pt sliders) and see how they affect the V-to-μ transform and thus, the "Expected Accuracy".

Note 1: The V-to-μ transform is modulated as a function of the global familarity (G) of the input, which is defined simply as the average maximum V value across the Q WTA competitive modules (CMs) that comprise a Sparsey coding field ("Mac"). This V-to-μ transform models the nonlinearity of a neuron and Sparsey is (to my knowledge) unique in proposing that the nonlinearity of the principal cells of a cortical representational field is modulated on-line and quickly, in fact, within a few, e.g., 5-10, ms (i.e., within a half-cycle of gamma), on the basis of a "mesoscale" measure of the subsuming coding field (e.g., the L2/3 population of a macrocolumn).

Note 2: The modulation of the V-to-μ transform, from a highly expansive sigmoid (when G ≈ 1, which means the input is maximally familiar, i.e., that it has likely been seen before) to the constant function (when G ≈ 0, which means the input is completely unfamiliar), can be viewed as modulating the amount of noise in the process of choosing winners in the CMs. I postulate that this variable "noise" mechanism is implemented by neuromodulators, e.g., ACh and NE (See 2010 paper).

The results below show how expected intersection size (as % of Q) decreases smoothly as the novelty of the current input increases (as the similarity of the current input to the closest matching stored input decreases). Seven experiments were run, using different parameter settings for V-to-μ transform. "mult" refers to the "range multiplier" slider in the app, "ecc" to the "sigmoid eccentricity" slider, and "inflect" to the "Horiz. Inflection Pt. Position" slider.  All experiments except the last used a Mac with Q=10 CMs each with K=8 units and min and max crosstalk limits of 10% and 30%; the last used Q=20 CMs, each wth K=10, and min and max crosstalk limits of 20% and 50%. The graded simiarlity preservation can be seen in all cases.

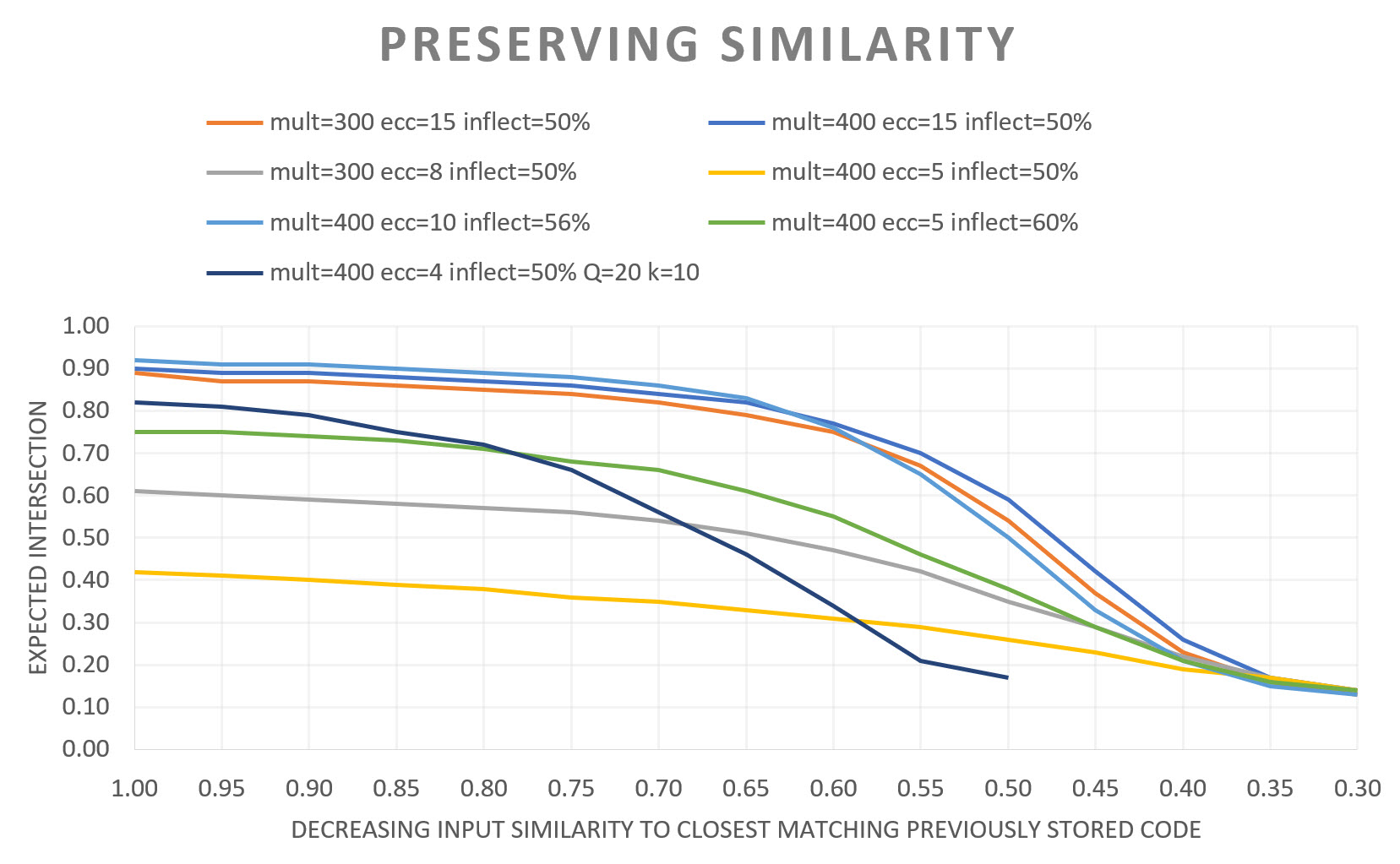
You can do many other things with the app as well. For instance, for any particular "Max V" (or equivalently, "G" setting), you can vary the other parameters, to see how they also cause smooth variation in the expected accuracy. Thus, it is not simply the V-to-μ transform range that we could modulate based on G, we could also choose to modulate these other parameters, e.g., sigmoid eccentricity, based on G. This is a subject of ongoing/future research. One interesting manipulation is explorable by playing with the "Phase of Life" buttons and is described below.

The "Phase of Life" buttons

The four "Phase of Life" radio buttons simulate conditions within a mac that might exist at different points of the system's lifetime. Since Sparsey's mac is an associative memory in which SDRs (memory traces) are stored in superposition, as more and more SDRs are stored, the expected intersection size over the stored SDRs will increase, thus crosstalk interference will increase. As noted above, the max V value (of one randomly chosen cell in each CM) is set by the user's setting of the "Max V" or "G" sliders (they are locked together). The rest of the cells in each CM are drawn from uniform distributions whose low and high limits are set either by the "Life Phase" buttons, or by the user setting the sliders at upper right (as was done in the video immediately above). Also, the user can choose whether those crosstalk distribution limits are determined relative to the currently spececified max V or "absolutely" (i.e., relative to the max possible max V, i.e., V=1).

• Early: The idea is that early in the model's life, when few memories have been stored, there will be little crosstalk (interference, overlap) between memory traces. To simulate this. the V values of the other cells are chosen randomly from the interval [0,0.1].
• Middle: In this case, the other V values are selected from the interval [0.1,0.5]. This simulates a later period of life after a lot more inputs have been stored and any given cell will have been used in the codes of many of those inputs.
• Late: The other cells' V values are chosen from interval [0.2,0.8], indicating mounting crosstalk between traces.
• Old: The model has stored so many traces that crosstalk is very high. Specifically, the K-1 other V values are chosen from interval [0.6,0.9].

A major principle to see here is that, for any given set of sigmoid parameters, increasing crosstalk reduces the expected number of CMs in which the cell with the highest V value ends up being chosen winner. When the input is perfectly familiar, i.e., when G=1, each such event constitutes an error, i.e., the wrong cell has been activated in the CM. However, a code consists of Q units; thus, making a few unit-level errors may still allow the code, as a whole, to exert the proper influence on downstream computations. More generally, the fact that in Sparsey, the Q units that comprise a code are chosen in independent processes is what allows for graded levels of similarity (intersection) between codes, i.e., the SISC property. Note that although we don't actually make the final winner choices in this video, the gradual flattening of the ρ distributions as one goes from "Early" to "Old", implies the graded reduction in the expected number of max-V cells that end up winning in their respective CMs.

So, what if we move the sigmoid inflection point, let's call that parameter Y, to the right as the coding field ages, i.e., as more and more SDR codes are stored in it and the level of crosstalk interference rises? For example, select "Old". You can see that expected accuracy is low. But if you then slide Y to the right, you can see that exepcted accuracy recovers. On the other had, suppose you select "Early". You will see highly peaked distributions in each CM [assuming you've populated the mac (see above)]. If you now slide the Y slider around, you will see that the range of Y for which the correct cells (those with the max V in their CM) have very high probability of winning is very large, extending from just over 10% up to 100%. Now select the "Middle" button. Note that the model can still ensure a high probability of reactivating the correct code, but that the range of Y for which this is the case has contracted to the right, typically spanning from about 50% to 100%. Click on "Late" and the range of Y yielding a high probability of success shrinks further. So, simply shifting the sigmoid's inflection point to higher V values recovers/preserves retrieval accuracy.

The question arises, why not simply keep Y at a high value througout the model's life? The answer is that there is a tradeoff involving Y. When Y is very high, then even fairly high V values will be squashed to near-zero ρ values. This greatly diminishes the propensity of the model to assign similar (i.e., more overlapped) codes to similar moments. Thus, the gradedness of the categories that the model would embed would be much reduced. Keeping Y at or near 100%, would simulate a person who stored almost all new experiences very uniquely, but was impoverished at forming categories based on similarity. Such a person would have very (i.e., too) strong episodic memory ability/capacity and weak semantic memory ability, perhaps something like a savant syndrome, e.g., Luria's famous patient S, "the mnemonist".

Y should depend on how saturated a regions's afferent synaptic matrices have become, i.e., what fraction of its synapses have been increased to the high setting, e.g., w=1, assuming binary synapses. I think that such a neurophysiological parameter would be quite easy for the brain to keep track of through the life of an organism. Moreover, it seems reasonable to believe that such a "degree of saturation" parameter could be maintained on a region-by-region (or macrocolumn-by-macrocolumn) basis across cortex. Thus, for example, the brain region(s) that are most used in storing the memory/knowledge of a given individual's particular field of expertise might fill up faster than other regions.

Sigmoid eccentricity parameter

The Sigmoid Eccentricity parameter simply controls how abruptly the the V-to-µ map changes from its low to its higher values. It also affects the granularity of the categories (spatial or spatiotemporal) formed by the model. However, we will not discuss it further here...except to repeat that it too can be modulated by G to achieve/enforce SISC.

Summary

The goal of this page and video and the downloadable Java app is to show how Sparsey's Code Selection Algorithm (CSA) achieves/enforces SISC extremely efficiently. It does so by transforming a local (cell-level) measure of support, V (essentially a cell's input summation, but normalized to [0.1]), over a competitive population of cells, using global (macrocolumn-level) information, G, into a distribution of relative likelihoods of becoming active (i.e., of winning the competition), μ, and then, by simple normalization, into a final probability distribution of winning, ρ. Crucially, this transform, specifically its range, is modulated by G in a way that results in enforcing that more similar inputs are mapped to more similar (more highly intersecting) SDCs.